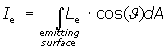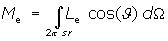The whole discipline of optical measurement techniques can be roughly subdivided into the two areas of photometry and radiometry. Whereas the central problem of photometry is the determination of optical quantities closely related to the sensitivity of the human eye (see § II.6.), radiometry deals with the measurement of energy per time ( = power, given in watts) emitted by light sources or impinging on a particular surface. Thus, the units of all radiometric quantities are based on watts (W). According to CIE regulations, symbols for radiometric quantities are denoted with the subscript "e" for "energy". Similarly, radiometric quantities given as a function of wavelength are labeled with the prefix "spectral" and the subscript "λ" (for example spectral radiant power Φ_λ).

Remark: The definitions of radiometric quantities cannot be understood without a basic comprehension of differential quantities. For an intuitive understanding of these quantities, which is the main purpose of this paragraph, the differential quantities dλ, dA and dΩ can be regarded as tiny intervals or elements ∆λ, ∆A and ∆Ω of the respective quantity. As a consequence of the fact that these intervals or elements are very small, radiometric quantities can be considered constant over the range defined by dλ, dA and/or dΩ. Similarly, dΦ_e, dI_e, dL_e and dE_e can be regarded as small portions which add up to the total value of the respective quantity. In paragraph II.5., the concept of differential quantities and integral calculus is briefly explained for spectral radiometric quantities.

II.4.a. Definition of solid angle
The geometric quantity of a solid angle Ω quantifies a part of an observer's visual field. If we imagine an observer located at point P, his full visual field can be described by a sphere of arbitrary radius r (see Fig.II.). Then, a certain part of this full visual field defines an area A on the sphere's surface and the solid angle Ω is defined by

Ω = A / r²

Equ. II.2

As the area A is proportional to r², this fraction is independent of the actual choice of r.

If we want to calculate the solid angle determined by a cone, as shown in Fig.II.area A is the area of a spherical calotte. However, as the solid angle is not only defined for conical parts of the full visual field, area A can be any arbitrary shape on the sphere's surface.

Although Ω is dimensionless, it is common to use the unit steradian (sr). The observer's total visual field is described by the whole surface of the sphere, which is given by 4πr², and thus covers the solid angle

Ω_total = 4πr² / r² = 4π sr = 12.57 sr

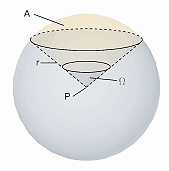
Fig.II.6. The solid angle Ω quantifies a certain part of the visual field, seen by an observer located at P

II.4.b. Radiant power or radiant flux Φ_e
Radiant power Φ_e is defined by the total power of radiation emitted by a source (lamp, light emitting diode, etc.), transmitted through a surface or impinging upon a surface. Radiant power is measured in watts (W). The definitions of all other radiometric quantities are based on radiant power. If a light source emits uniformly in all directions, it is called an isotropic light source.

Radiant power characterizes the output of a source of electromagnetic radiation only by a single number and does not contain any information on the spectral distribution or the directional distribution of the lamp output.



Fig. II.7. The radiant power of Φ_e of a light source is given by its total emitted radiation.


II.4.c. Radiant intensity I_e
Radiant intensity I_e describes the radiant power of a source emitted in a certain direction. The source's (differential) radiant power dΦ_e emitted in the direction of the (differential) solid angle element dΩ is given by

dΦ_e = I_e dΩ

and thus



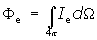
In general, radiant intensity depends on spatial direction. The unit of radiant intensity is W/sr.



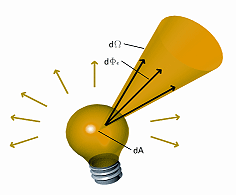
Fig. II.8. Typical directional distribution of radiant intensity for an incandescent bulb.

II.4.d. Radiance L_e
Radiance L_e describes the intensity of optical radiation emitted or reflected from a certain location on an emitting or reflecting surface in a particular direction (the CIE definition of radiance is more general. Within the frame of this tutorial, the most relevant application of radiance describing the spatial emission characteristics of a source is discussed ). The radiant power dΦ_e emitted by a (differential) surface element dA in the direction of the (differential) solid angle element dΩ is given by

dΦe = Le cos(J) dA dΩ

Equ.II.3

In this relation, λ is the angle between the direction of the solid angle element dΩ and the normal of the emitting or reflecting surface element dA.

From the definition of radiant intensity I_e it follows that the differential radiant intensity emitted by the differential area element dA in a certain direction is given by

dI_e = L_e cos(J) dA

Thus,

Equ.II.4

whereby J is the angle between the emitting surface element dA and the direction for which I_e is calculated.

The unit of radiance is W/(m².sr).

II.4.e. Irradiance E_e
Irradiance E_e describes the amount of radiant power impinging upon a surface per unit area. In detail, the (differential) radiant power dΦ_e upon the (differential) surface element dA is given by

dΦ_e = E_e dA

Generally, the surface element can be oriented at any angle towards the direction of the beam. However, irradiance is maximised when the surface element is perpendicular to the beam:

dΦ_e = E_e,normal dA _normal



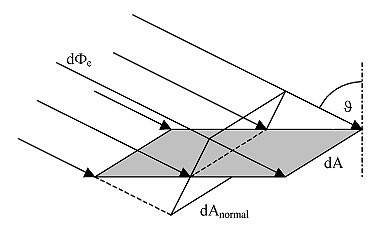
Fig. II.9 — Irradiance is defined as incident radiant power dΦ_e per surface area element dA.

Note that the corresponding area element dA _normal, which is oriented perpendicular to the incident beam, is given by

dA _normal = cos(J) dA

with λ denoting the angle between the beam and the normal of dA, we get

Ee = Ee,normal cos(J)

Equ.II.5

The unit of irradiance is W/m².

II.4.f. Radiant exitance M_e
Radiant exitance M_e quantifies the radiant power per area, emitted or reflected from a certain location on a surface. In detail, the (differential) radiant power dΦ_e emitted or reflected by the surface element dA is given by

dΦ_e = M_e dA

From the definition of radiance follows that the (differential) amount radiant exitance dM_e emitted or reflected by a certain location on a surface in the direction of the (differential) solid angle element dΩ is given by

dM_e = L_e cos(J) dΩ

and consequently

Equ.II.6

The integration is performed over the solid angle of 2π steradian corresponding to the directions on one side of the surface and J denotes the angle between the respective direction and the surface's normal.

The unit of radiant exitance is W/m². In some particular cases, M_e= E_e (see § II.8.a).

II.4.g. Spectral radiant power Φ_λ(λ), spectral radiant intensity I_λ(λ), spectral radiance L_λ(λ), spectral irradiance E_λ(λ), and spectral radiant exitance M_λ(λ)
The radiometric quantities discussed above are defined without any regard to the wavelength(s) of the quantified optical radiation. In order to quantify not only the absolute amount of these quantities but also the contribution of light from different wavelengths, the respective spectral quantities are defined.

Spectral radiant power is defined as a source's radiant power per wavelength interval as a function of wavelength. In detail, the source's (differential) radiant power dΦ_e emitted in the (differential) wavelength interval between λ and λ+dλ is given by

dΦ_e = Φ_λ(λ) dλ

This equation can be visualised geometrically (see Fig. II.10.). As dλ is infinitesimally small, spectral radiant power Φ_λ(λ) is approximately constant in the interval between λ and λ+dλ. Thus, the product Φ_λ(λ) dλ equals the area under the graph of Φ_λ(λ) in the interval between λ and λ+dλ. This area describes the contribution of this very wavelength interval to the total value of radiant power Φ_e, which is graphically represented by the total area under the graph of spectral radiant power Φ_λ(λ).

Mathematically, this can be expressed by the integral



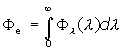
The unit of spectral radiant power is W/nm or W/Å.



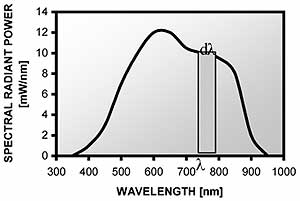
Fig.II.10. Relation between spectral radiant power Φ_λ(λ) and radiant power Φ_e, visualized at a hypothetical example. Radiant power emitted in the wavelength interval between λ and λ+dλ is given by the area of the shaded rectangle, which amounts to Φ_λ(λ) dλ. The total amount of radiant power Φ_e emitted over the whole spectrum is given by the area under the curve describing Φ_λ(λ), which is mathematically expressed by an integral.

The other spectral quantities are defined correspondingly and their units are given by the unit of the respective quantity, divided by nm or Å (seeTable VII.IV and Table VII.V). Generally, a radiant quantity can be calculated from the respective spectral quantity by integration over wavelength from λ=0 to λ=∞. However, this integration is often restricted to a certain wavelength range, which is indicated by the respective prefix. For instance, UVA irradiance is defined as



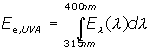
as the UVA range is defined from λ= 315 nm to λ = 400 nm.