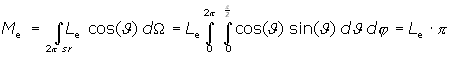II.5. Calculation of radiometric quantities - Examples
II.5.a. Example 1: Isotropic point source
A small source emits light equally in all directions (spherical symmetry). Its radiant power equals Φe,source=10 W.
If we are interested in the characteristics of this source in a distance r that is much larger than the geometric dimensions of the source itself, we can neglect the actual size of the source and assume that the light is emitted from a point. As a rule of thumb, this approximation is justified if distance r is at least 10 times larger than the dimensions of the light source.
a/ As the source emits light symmetrical in all directions, its radiant intensity is equal for all directions and amounts to
Ie = Φe,source / 4π sr = 10 W / 4π sr = 0.796 W / sr.
b/ An infinitesimal surface element dA at distance r and perpendicular to the beam occupies the solid angle
dΩ = dA / r²
and thus the infinitesimal radiant power dΦe,imp impinging onto dA can be calculated by
dΦe,imp = I dΩ = Φe,source / 4π sr · dA / r² = Φe,source / 4πr² · dA
Thus, the irradiance at distance r amounts to
Ee = Φe,source / 4πr²
This result can also be obtained by the following argument:
At distance r, all the radiant power Φe,source emitted by the source passes through the surface of a sphere with radius r, which is given by 4r²π. As the light source emits light symmetrically in all directions, the irradiance has the same value at every point of this sphere. Thus, irradiance E of a surface at a certain distance r and oriented perpendicular to the beam can be calculated from its definition:
Ee = radiant power impinging upon a surface / area of this surface = Φe,source / 4πr²
which is identical with the result above.
Remark: The fact that E is proportional to r-² is generally known under the name "inverse square law". However, it only holds true for distances much larger than the geometric dimensions of the source, which allows the assumption of a point source. In other cases, a source with considerable geometric dimensions might possibly be replaced by a "virtual" point source, and then the "inverse square law" still holds true when distance r is measured from this virtual point source (see Example 2). However, when the source cannot be assumed point like and every point of the source emits light in more than a single direction , the "inverse square law" no longer holds true. As an example, this is the case for fluorescent tubes.
II.5.b. Example 2: Spot source
In a simple flashlight, a concave mirror reflects light from a small bulb (radiant power Φ = 200 mW) into a divergent cone (see figure below). Assuming that the mirror reflects without any losses and uniform distribution of power over the cone,
Note that the flashlight does not emit light symmetrically in all directions, therefore the equations derived in Example 1 cannot be used.
a/ In a distance of 25 cm from the flashlight's front window, the whole radiant power of 200 mW ( = 0.2 W) impinges on a circle with a radius of 0.05 m. If we assume that irradiance is constant all over this circle and we neglect the fact that the surface is not everywhere strictly perpendicular to the beam, we can calculate the irradiance at a distance of 25 cm from the flashlight's front window:
E = radiant power impinging upon a surface / area of this surface == 0.2 / 0.05² π W / m²
E ≈ 25 W / m²
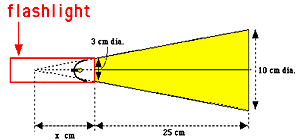
Fig. II.11 - Calculating the irradiance caused by a flashlight.
b/ In order to determine the flashlight's radiant intensity, we have to determine the solid angle determined by the cone. Following the definition of solid angle and approximating the area of the spherical calotte by the area of a circle with a radius of 5 cm (= 0.05 m), we get
Ω = ACircle / r²
with r describing the distance of the circle form the cone's vertex.
From Fig. II.11, we get
r = x + 0.25 m
and
x / x + 0.25 = 0.03 / 0.10
from which we calculate
x = 0.107 m
and
r = 0.357 m
Thus, the cone defines a solid angle given by
Ω = ACircle / r² = 0.05² π / 0.357² = 0.0616 sr
and the flashlight's radiant intensity amounts to
I = Φ / Ω = 0.2 / 0.0616 W / sr = 3.25 W / sr.
Remark: As a virtual point source located at the cone's vertex produces the same spatial radiation distribution as the flashlight's bulb together with its concave mirror, the "inverse square law" holds true for this configuration. However, the distance r which the law relates to has to be measured from the position of the virtual point source.
II.5.c. Example 3: The Lambertian surface
By definition, a Lambertian surface either emits or reflects radiation into all directions of a hemisphere with constant radiance Le (Fig.II.12). From Equ.II.4 in paragraph II.4.d. follows that the directional distribution of radiant intensity is given by
Ie(J) = Ie,0 · cos(J) with I 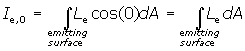
whereby Ie,0 denotes radiant intensity emitted in the direction perpendicular to the surface and Ie(J) denotes radiant intensity emitted in a direction enclosing the angle J with the surface's normal. Calculating the surface's exitance Me from Equ.II.6 in paragraph II.4.f. by use of the relation dΩ = sin(J) dJ dφ, we get
|
|
Equ. II.7 |
The respective relations for photometric quantities (see § II.6.) characterising a Lambertian surface can be derived by replacing the index "e" by the index "v".
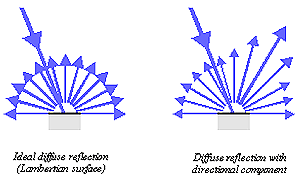
Fig.II.12. Constant spatial distribution of radiance Le after ideal diffuse reflection at a Lambertian surface
Reflecting Lambertian surfaces are widely used in light measurement for well defined, perfectly diffuse scattering fully independent of the direction of the incoming beams. Thus, the radiance reflected from a certain location on the surface in a certain direction is proportional to the total radiant power impinging onto the reflecting surface. This allows the realisation of detector geometries for radiant power, exitance and irradiance (or luminous flux, luminous exitance and illuminance), which have to be determined by an integration over all directions of a solid angle of 4π or 2π. Lambertian reflection is especially desired for the coating of integrating spheres, which are widely used for detector input optics or for output optics of radiance or luminance standards.
Tutorials