Like all other waves (waves in a string, water waves, sound, earthquake waves ...), light and electromagnetic radiation in general can be described as a vibration (more general: a periodical change of a certain physical quantity) that propagates into space (Fig. II.4.a). The propagation is caused by the fact that the vibration at a certain location influences the region next to this location. For example in the case of sound, the alternating rarefaction and compression of air molecules at a certain location results in periodic changes in the local pressure, which in turn causes the movement of adjacent air molecules towards or away from this location (Fig. II.4.b).

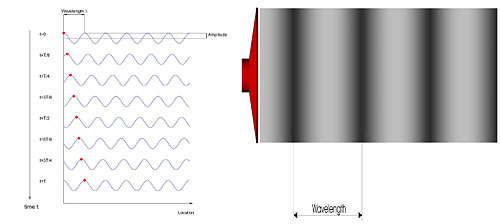
Fig. II.4 (a) Formation and propagation of a wave in a string. (b) Formation and propagation of a compression wave in air, a phenomenon colloquially called sound

In the case of an electromagnetic wave, the mechanism of propagation involves mutual generation of periodically varying electric and magnetic fields and is far more difficult to understand than sound. Yet, the result still can be described as a periodic change of a physical quantity (the strength of the electric and the magnetic field) propagating into space. The velocity of this propagation is generally abbreviated with the letter c (unit: meters per second, m/s) and depends on the nature of the wave and on the medium (see Table II.I below).

	Sound	Optical (electromagnetic) radiation
		at λ=434 nm	at λ=589 nm	at λ=656 nm
in vacuum	-	299792 km/s (n = 1)	299792 km/s (n = 1)	299792 km/s (n = 1)
in air	340 m/s	299708 km/s (n = 1.000280)	299709 km/s (n = 1.000277)	299710 km/s (n = 1.000275)
in water	1500 m/s	223725 km/s (n = 1.340)	224900 km/s (n = 1.333)	225238 km/s (n = 1.331)

Table II.I Velocities of sound and light in air and in water. For optical radiation, the respective index of refraction is given in parenthesis

In order to describe the basic properties of a wave, the following quantities have been defined for all kinds of waves:

• The amplitude is the maximum disturbance of the medium from its equilibrium. In the case of a wave in a horizontal string (Fig. II.4.a), this value is identical with half of the vertical distance between the wave's crest and its trough. In the case of a pressure wave in air ("sound", Fig. II.4.b), the amplitude is half of the pressure difference between rarefaction and compression.
• The wavelength λ is the distance between two adjacent crests (or troughs) and is given in meters.
• The period T of a wave is the time that elapses between the arrival of two consecutive crests (or troughs) at a certain location X. This definition is identical with the statement that the period is the time the vibration at X takes to complete a full cycle from crest to trough to crest. The period of a wave is given in seconds.
• The frequency ν of a wave is the number of vibration cycles per second at a certain location X. The unit of frequency is Hertz (Hz) and 1 Hz is the reciprocal of 1 second. As an example, a wave with a period T = 0.25 s takes ¼ of a second to complete a full vibration cycle (crest - trough - crest) at a certain location and thus performs four vibrations per second. Hence its frequency is f = 4 Hz. From this example it is obvious that the period of a wave completely defines its frequency and vice versa. The relation between these quantities is given by

ν = 1 / T

If we look at a wave as a process that is periodical in space and in time, we can regard the wavelength λ as the distance between two repetitions of the process in space and the period T as the "distance" between two repetitions of the process in time.

A basic relation between wavelength, frequency and velocity results from the following consideration:

During the time span a crest needs to travel the distance of one wavelength λ from location X to location Y (Fig. II.4.a), the next crest arrives at location X. Thus, this time span is identical with the wave's period T. But when a crest needs the time span T to travel the distance λ, its velocity c amounts to

c = λ / T = λ .ν     Equ. II.1

When a wave passes from one medium to another, its frequency remains the same. If the velocities of the wave in the two media differ, the wavelengths in the two media also differ as a consequence of equation II.1.

As the frequency of a wave does not depend on the medium the wave is passing, it is more convenient to use frequency instead of wavelength to characterise the wave. In acoustics, this is common practice — in most cases the pitch of sound is characterised by its frequency instead of its wavelength in a certain medium (for example air).

In optics, the situation is different: In most cases wavelength is used instead of frequency, although this leads to a certain complication: For example, green light has a wavelength of 520 nm in vacuum, but in water its velocity is smaller by a factor of 1.33 and thus, in water the same green light has a wavelength of only 520 / 1.33 = 391.0 nm. Hence, if we want to characterize a wave by its wavelength, we also have to state for which medium the actual wavelength value is given. According to CIE regulations, which are also applied throughout this tutorial, the term "wavelength" refers to "wavelength in air" unless otherwise stated. However, when applying the given wavelength figures to light passing through a medium other than vacuum, one should keep in mind that the light's wavelength changes according to the relation

λ_Medium = λ_Vacuum / n_Medium = λ_Air · n_Air / n_Medium

with

n_Air = c_Vacuum / c_Air and n_Medium = c_Vacuum / c_Medium

n_Medium is called the medium's index of refraction and is more commonly used to specify the optical properties of a material than c_Medium