The basic problem of colorimetry is the quantification of the physiological color perception caused by a certain spectral color stimulus function j_l(l). When the color of a primary light source has to be characterised, j_l(l) equals the source's spectral radiant power F_l(l) (or another spectral radiometric quantity, such as radiant intensity or radiance). When the color of a reflecting or transmitting object (for example a filter) has to be characterised, j_l(l) equals the incident spectral irradiance impinging upon the object's surface, multiplied by the object's spectral reflectance, its spectral radiance coefficient or its spectral transmittance. As colors of reflecting or transmitting objects depend on the object's illumination, the CIE has defined colorimetric standard illuminants. The CIE Standard Illuminant A is defined by a Planckian blackbody radiator at a temperature of 2856 K, and the CIE Standard Illuminant D₅₆ is representative of average daylight with a correlated color temperature of 6500 K (for the definition of color temperature, see below).

II.10.a. RGB and XYZ color matching functions
According to the tristimulus theory, every color which can be perceived by the normal sighted human eye can be described by three numbers which quantify the stimulation of red, green and blue cones. If two color stimuli result in the same values for these three numbers, they produce the same color perception even when their spectral distributions are different. Around 1930, Wright and Guild performed experiments during which observers had to combine light at 435.8 nm, 546.1 nm and 700 nm in such a way that the resulting color perception matched the color perception produced by monochromatic light at a certain wavelength of the visible spectrum. Evaluation of these experiments resulted in the definition of the standardised RGB color matching functions 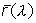,  and 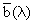, which have been transformed into the CIE 1931 XYZ color matching functions 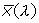,  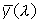and . These colour matching functions define the CIE 1931 standard colorimetric observer and are valid for an observer's field of view of 2°. Practically, this observer can be used for any field of view smaller than 4°. 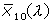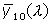For a field of view of 10°, the CIE specifies another set of colour matching functions ,  and 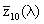. This set defines the CIE 1964 supplementary standard colorimetric observer, which has to be used for fields of view larger than 4°.



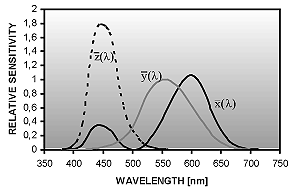
Fig. II.21 - XYZ color matching functions as defined by the CIE 1931 standard colorimetric observer. 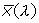 (solid black line) consists of a short- and a long-wavelength part, and 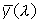 (solid grey line) is identical with the CIE spectral luminous efficiency function V(ë).

Although RGB and XYZ color matching functions can be equally used to define three parameters which numbers uniquely describe a certain color perception, the XYZ color matching functions are preferred as they have positive values for all wavelengths (Fig. ). In addition, 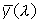 is equal to the CIE spectral luminous efficiency function V(ë) for photopic vision.

The XYZ tristimulus values of a certain spectral color stimulus function j_l(l) are calculated by



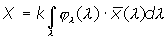
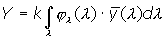
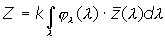
The choice of the normalisation constant k depends on the colorimetric task: When the spectral color stimulus j_l(l) describes a spectral radiometric quantity of a primary light source, k = 683 lm/W and consequently Y yields the corresponding photometric quantity. When the spectral color stimulus j_l(l) describes the spectral distribution of optical radiation reflected or transmitted by an object, k is defined by



with E(ë) denoting the incident spectral irradiance impinging upon the object's surface.

II.10.b. The (x,y)- and (u',v')-chromaticity diagrams
Although the XYZ tristimulus values define a three-dimensional color space representing all possible color perceptions, for most applications the representation of color in a two-dimensional plane is sufficient. One possibility for a two-dimensional representation is the CIE 1931 (x, y) chromaticity diagram with its coordinates x and y calculated from a projection of the X, Y and Z values:




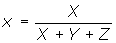
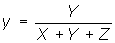
Although widely used, the (x, y) chromaticity diagram has a major disadvantage of non-uniformity as geometric distances in the (x, y) chromaticity diagram do not correspond to perceived color differences. Thus, in 1976 the CIE defined the uniform (u', v') chromaticity scale (UCS) diagram, with its coordinates defined by





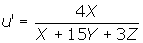
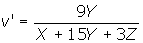
Although this definition of the coordinates u' and v' does not provide a strict correspondence between geometric distances and perceived color differences, there are far less discrepancies than in the CIE (x, y) chromaticity diagram.


Fig. II.22 - The CIE 1931 (x,y) chromaticity diagram and the CIE 1976 (u', v') chromaticity diagram.

II.10.c. Correlated color temperature
The correlated color temperature is used to characterize the spectral distribution of optical radiation emitted by a light source. This characterisation corresponds to the projection of a two-dimensional chromaticity diagram onto a one-dimensional scale and thus is very coarse.

In detail, the correlated color temperature is given in Kelvin (K) and is the temperature of the blackbody (Planckian) radiator whose received color most closely resembles to that of a given color stimulus.

As a (simplified) rule of thumb, spectral distributions dominated by long (reddish) wavelengths correspond to a low correlated color temperature whereas spectral distributions with dominated by short (bluish) wavelengths correspond to a high correlated color temperature. As an example, the warm color of incandescent lamps has a correlated color temperature of about 2800 K, average daylight has a correlated color temperature of about 6500 K and the bluish white from a Cathode Ray Tube (CRT) has a correlated color temperature of about 9000 K.